理想光学系统下物像关系分析及应用

在视觉检测装置中，图像采集组要由相机和镜头完成，为得到一张理想的图像，需要合理选择相机及镜头。在工作中相机的选择一般根据所需的图像分辨率即可确定型号。而镜头的选择则需根据工件尺寸（视野）及安装空间（物距）综合选定，有多种组合情况。
在实际工作中，一般会根据实际应用经验，将常用镜头的视野与物距编制成视野表，以便在需要时进行查阅。通过视野表选择镜头会比较准确，但需一一查找，效率较低。为提高效率，可通过镜头成像公式进行计算得到。本文即对此计算公式进行简单说明。
一、理想光学系统
工业镜头结构如图二所示，是由多组镜片组合而成，多镜片组合光路计算比较复杂，而镜头的最终效果是体现为凸透镜的，故为了进行估算，可将其简化为一个凸透镜，采用理想光学系统模型进行分析。
图一 镜头结构
图二 理想光学系统的物像关系
在几何光学中，所谓的理想光学系统，就是对足够大空间内的各个点能以足够宽光束成完善像、理想像的光学系统。在各向同性的均匀介质中，理想光学系统的物像关系应具备以下特性：
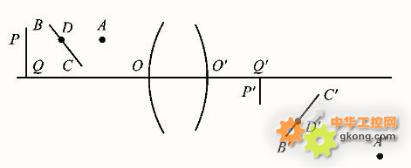
1、点成点像：即对于物空间的每一点，在像空间必有一个点与之相对应，且只有一个点与之对应，这样的两个对应点称为物像空间的共轭点（如图一中的A点和A′点）；
2、线成线像：即对于物空间的每一条直线，在像空间必有一条直线与之相对应，且只有一条直线与之对应，这样的两条对应直线称为物像空间的共轭线（如图一中的BC和B′C′）；
3、平面成平面像：即物空间的每一个平面，在像空间必有一个平面与之相对应，且只有一个平面与之对应，这样的两个对应平面称为物像空间的共轭面（如图一中的PQ面和P′Q′面）。
二、理想光学系统下物像关系解析
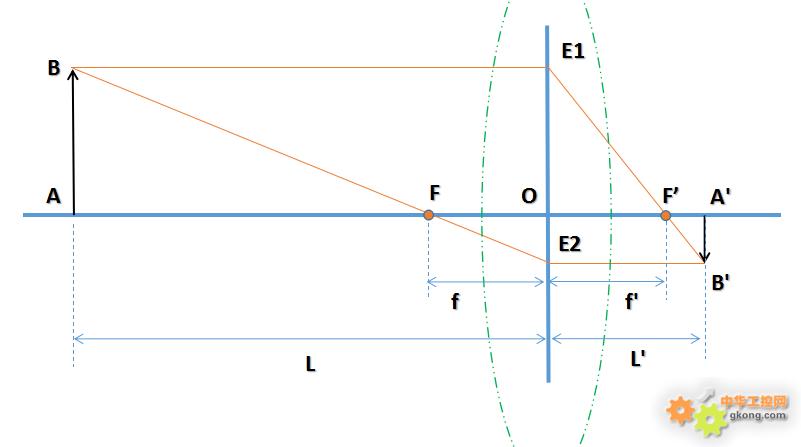
图三
在图三中，E1E2为理想透镜中轴线，AA’为穿过透镜中心的光轴，与E1E2交于O点，F、F’为焦点。
根据理想光学系统物像关系，设透镜外一垂直于光轴AA’的线段端点B发出两条特定光线，一条由点B发出通过焦点F，与透镜中轴交于E2，经透镜折射后的光线平行于光轴；另一条光学由点B发出平行于光轴，与透镜中轴交于E1点，经透镜折射后的光线将通过像方焦点F’。在像空间这两条光线的交点B’即为点B的像点。过点B’作光轴的垂线B’A’，即为物AB的像。
1、物高H、物距L、像高h、与焦距f之间的关系。
对图三光路进行分析可知，三角形ABF与三角形FOE2互为相似三角形，且B’A’=OE2，故A’B’：AB=OF：AF=f：（L-f），即f/(L-f)=h/H。
2、物高H、像距l、像高h、与焦距f之间的关系
对图三光路进行分析可知，三角形E1E2F’与三角形F’A’B互为相似三角形，且AB=E1E2，故A’B’：E1E2=AF：OF’=（L’-f’）：f’=h:H，因f=f’，所以f/l=H/(H+h)。
通过以上两组关系式，即可依据其中三个参数，快速估算得到第四个参数的值，在进行镜头选型或视觉系统装配关系时，获得参考。